Editor’s Question Answered: Incubator Temperature Control

Do you know how your incubator works?  Does it matter?  In the case where there’s a choice about where to put the thermostat probe, it can matter a whole lot:

Question

My incubator measures approximately 24″x24″x24″.  It has a digital thermostat with a probe inside the incubator that I can put anywhere in the incubator I want.  It has a setting that tells it to turn on or off when it gets to be more than 0.5 degrees F above or below the set temperature of 82.5.

Inside the incubator I have a sealed plastic egg container measuring approx. 4″x6″x6″ with a moist interior that maintains high humidity.

I put the thermostat probe on the incubator shelf.  I have a digital readout of the temperature that the probe records and that ranges from 82.4-83.3.  I have a digital thermometer with a probe inside the egg box and that remains steady at 82.6.

Here’s my question:  When I put the thermostat probe inside the egg box, I would expect that the temperature would remain even steadier, however, the temperature fluctuates more widely and takes longer to change.  Why is that?

Answer

Heat can be added to a system, removed from a system, or transferred between systems. When heat is transferred from system 1 to system 2, the heat lost by system 1 is equivalent to the heat gained by system 2. Your incubator can be thought of entirely in terms of heat transfers. Heat is transferred from the heating element in the incubator, to the air in the incubator. At the same time, heat is also being transferred from the air in your incubator to the air in your living room, since the incubator is not perfectly insulated. Finally, there is also a heat transfer going on between the air in your egg box and the air in the incubator. Heat transfer is expressed in Newton’s law of cooling as: dQ/dt=h*A*(Tsystem-­‐Tenvironment), where h is a constant that depends on how well insulated the two systems are, and A is the surface area between the systems. In other words, the rate of heat transfer between the two systems is proportional to the difference in temperature between the two systems.

Newton’s law of cooling is pretty intuitive. To put it in the context of your example, it states the following: If the temperature of the air in your incubator is much greater than the temperature of your egg box, heat will flow from the air in the incubator to the air in your egg box very quickly. If the air temp in the incubator is slightly higher than the temp in your egg box, heat transfer will be slower. If the air temp in your incubator is the same as the air temp in your egg box, then no heat will be transferred between the 2.

The last thing to keep in mind before continuing is that a heat transfer is not exactly the same thing as an increase in temperature. Since nothing is boiling or freezing in your systems, we can say that Q=m*c*ΔT, where Q is the heat added to a system, m is the mass of the system, c is the specific heat (heat capacity) of the system, and ΔT is the temperature increase of the system. An example to illustrate the difference between heat addition and temperature increase is as follows: system 1 has a mass of 1lb, and system 2 has a mass of 2lb. The heat capacity of both systems is equivalent. If the same amount of Q is added to both systems, then the temperature increase seen by the first system will be twice as large as the temperature increase seen by the second system.

Now lets consider the set­‐up that you have. The first step is to break it down into systems that we can analyze separately. In your case, one system is the air inside the incubator, and another system is the humid air inside the egg box. We could define the heating element as a separate system, but that will complicate things a little more, so lets consider it to be part of the system that consists of the air inside your incubator.

Now that the systems are defined, we can see what will happen to each system under certain circumstances. First consider the case where the probe is inside the incubator. Let’s start at a point in time where the temperature of the egg box and the incubator are both below the desired 82.5 degrees. At this point, the heating element will be activated, and heat will be added to the air in your incubator, thus increasing the temperature of the air in the incubator. Heat will also be transferred from the air in your incubator to the humid air inside of your egg box. The temperature of your egg box will rise, but it won’t rise quite as quickly as the temp of the air in the incubator because it is insulated, and it probably has more mass (due to the water content). If you plot temperature of the two systems vs. time, your graph will look something like this:

fig A-­‐1

Now that the 82.5 degree limit has been reached, your heating element will be shut off. Your heating element is now shut off, but it is still giving heat to the air in your incubator because its temperature is greater than the temperature of the air in your incubator. The result will be that the air temp in your incubator will continue to rise past the 82.5 degree threshold, until the heat being lost to the surroundings (the living room and the egg box) is equivalent to the heat being added by the heating element. Since our incubator air temp is still rising, your egg box temp will also continue to rise. Your new graph will look like this:

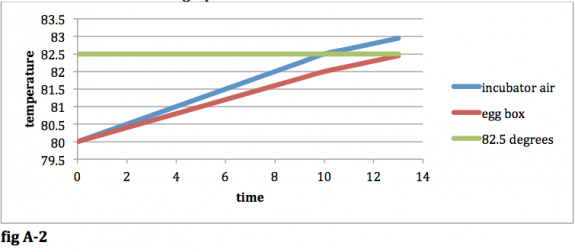
fig A-­‐2

Now, the air in your incubator is losing heat to the surroundings faster than it is gaining heat from the heating element, so its temperature will begin to decrease. The temperature will continue to decrease until it drops below 82.5 degrees. At this point, the heating element will be re‐engaged and the temperature of the incubator will rise again. In the long run, the temperature of the air in your incubator will oscillate around the 82.5 degree threshold. The temperature of the air in your egg box will also oscillate, but it will stay closer to the 82.5 degree threshold because it is insulated from your incubator air (thus decreasing the rate of heat transfer), and it has more mass than the air in your incubator (thus decreasing the temp increase per amount of heat transferred). Your result will look like this:

fig A-­‐3

Now, consider a case where the temperature probe is in the egg box. Start all systems at a temperature lower than 82.5 degrees. Your heating element will be activated until the temperature of your egg box reaches the required 82.5 degrees. Here are the results of the initial increases in temperature:

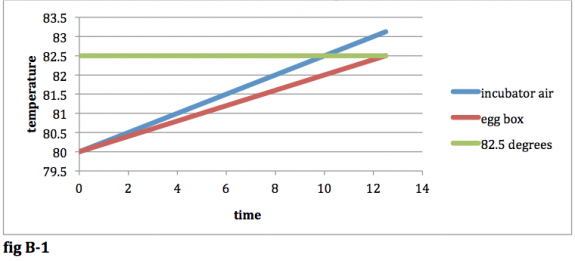
fig B-­‐1

Compare fig B-­‐1 with fig A-­‐1. Since you have to wait for the temperature of the egg box to hit 82.5 degrees, the temp of the incubator air in B-­‐1 is higher than that in A-­‐ 1. Both of these figures represent the point in time when the heating element is shut off. As described before, once the heating element is shut off, the air in the incubator will still increase in temperature. Once the rate of heat loss by the incubator air is equal to the rate of heat gained by the air, you will have something that looks like this:

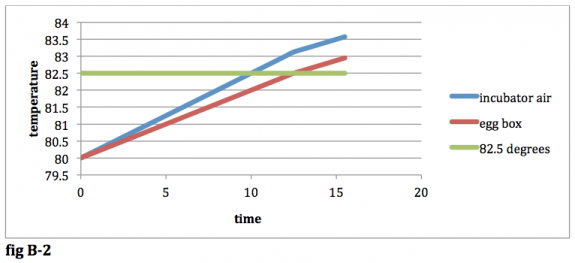
fig B-­‐2

At this point in time, the temperature of the air in the incubator will begin to decrease. The temperature of the air in the egg box however will continue to increase until it reaches the same temperature as the air in the incubator. The results until the two temperatures are equal will look like this:

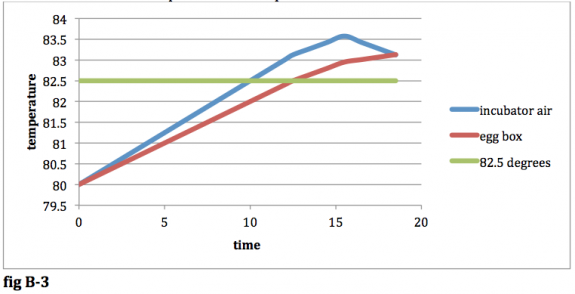
fig B-­‐3

In the long run, the temps will oscillate just as they did before, but the amplitude of the oscillation will be greater for both the egg box and the incubator air:

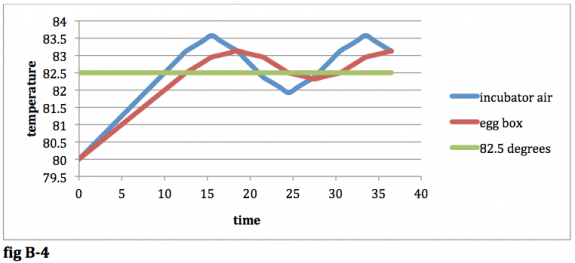
fig B-­‐4

If the probe needs to be in the egg box for some reason, then you could control the temperature more accurately by reducing the amount of insulation, or by decreasing the amount of mass in the egg box by decreasing volume or humidity. If the probe is outside of the egg box for your application (constant temp desired), it makes sense to have a high mass and a high level of insulation in the egg box so that the egg box temp will not fluctuate as much with the temp of the air in the incubator. For an application where you want the temperature to be changing with respect to time (say you want to use your incubator to simulate how the temperature outside changes over the course of a day), then you may want to have low mass and low insulation in your egg box.

Note: these graphs were made in excel. Nicer looking ones could be made with better software.